Selasa, 04 Desember 2012

turunan

18.24    No comments

Turunan

!Artikel utama untuk bagian ini adalah: Turunan
Grafik fungsi turunan.
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.

Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
f'(x)=\lim_{h \to 0}{f(x+h) - f(x)\over{h}} ,
dengan syarat limit tersebut eksis. Jika ƒ′ eksis pada titik x tertentu, kita katakan bahwa ƒ terdiferensialkan (memiliki turunan) pada x, dan jika ƒ′ eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.
Apabila z = x + h, h = z - x, dan h mendekati 0 jika dan hanya jika z mendekati x, maka definisi turunan di atas dapat pula kita tulis sebagai:
f'(x)=\lim_{z \to x}{f(z) - f(x)\over{z-x}}

Garis singgung pada (x, f(x)). Turunan f'(x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.
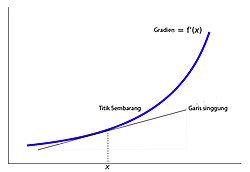
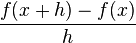Perhatikan bahwa ekspresi {f(x+h) - f(x)\over{h}} pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
Sebagai contoh, untuk menemukan gradien dari fungsi f(x)=x^2 pada titik (3,9):
\begin{align} f'(3)&=\lim_{h \to 0}{(3+h)^2 - 9\over{h}} \\ &=\lim_{h \to 0}{9 + 6h + h^2 - 9\over{h}} \\ &=\lim_{h \to 0}{6h + h^2\over{h}} \\ &=\lim_{h \to 0} (6 + h) \\ &= 6 \end{align}
Ilmu yang mempelajari definisi, properti, dan aplikasi dari turunan atau kemiringan dari sebuah grafik disebut kalkulus diferensial
Garis singgung sebagai limit dari garis sekan. Turunan dari kurva f(x) di suatu titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.

Notasi pendiferensialan

Terdapat berbagai macam notasi matematika yang dapat digunakan digunakan untuk menyatakan turunan, meliputi notasi Leibniz, notasi Lagrange, notasi Newton, dan notasi Euler.
Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi tersebut terhadap x ditulis sebagai:
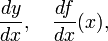\frac{dy}{dx},\quad\frac{d f}{dx}(x),  ataupun  \frac{d}{dx}f(x).
Notasi Lagrange diperkenalkan oleh Joseph Louis Lagrange dan merupakan notasi yang paling sering digunakan. Dalam notasi ini, turunan fungsi ƒ(x) ditulis sebagai ƒ′(x) ataupun hanya ƒ′.
Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila y = ƒ(t), maka \dot{y} mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.
Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk memberikan turunan pertamanya Df. Apabila y = ƒ(x) adalah variabel terikat, maka sering kali x dilekatkan pada D untuk mengklarifikasikan keterbebasan variabel x. Notasi Euler kemudian ditulis sebagai:
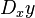D_x y\,   atau   D_x f(x)\,.
Notasi Euler ini sering digunakan dalam menyelesaikan persamaan diferensial linear.

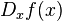 Notasi Leibniz Notasi Lagrange Notasi Newton Notasi Euler
Turunan ƒ(x) terhadap x \frac{d}{dx}f(x) ƒ′(x) \dot{y}
dengan y = ƒ(x)		 D_x f(x)\,

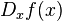0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)