Limit dan kecil tak terhingga

Artikel utama untuk bagian ini adalah:
Limit

Definisi limit: kita katakan bahwa limit f(x) ketika x mendekati titik p
adalah L apabila untuk setiap bilangan ε > 0 apapun, terdapat
bilangan δ > 0, sedemikian rupanya:

Kalkulus pada umumnya dikembangkan dengan memanipulasi sejumlah
kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan sebagai
angka, adalah sangat kecil. Sebuah bilangan
dx yang kecilnya tak
terhingga dapat lebih besar daripada 0, namun lebih kecil daripada
bilangan apapun pada deret 1, ½, ⅓, ... dan bilangan real positif
apapun. Setiap perkalian dengan kecil tak terhingga (infinitesimal)
tetaplah kecil tak terhingga, dengan kata lain kecil tak terhingga tidak
memenuhi
properti Archimedes. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak terhingga.
Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena tidak cukup cermat, sebaliknya ia digantikan oleh konsep
limit.
Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan
hasil dari nilai input terdekat. Dari sudut pandang ini, kalkulus adalah
sekumpulan teknik memanipulasi limit-limit tertentu. Secara cermat,
definisi limit suatu fungsi adalah:
Diberikan fungsi f(x) yang terdefinisikan pada interval di sekitar p, terkecuali mungkin pada p itu sendiri. Kita mengatakan bahwa limit f(x) ketika x mendekati p adalah L, dan menuliskan:
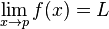
jika, untuk setiap bilangan ε > 0, terdapat bilangan δ > 0 yang
berkoresponden dengannya sedemikian rupanya untuk setiap x:
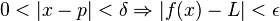


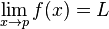
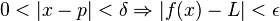















0 komentar:
Posting Komentar